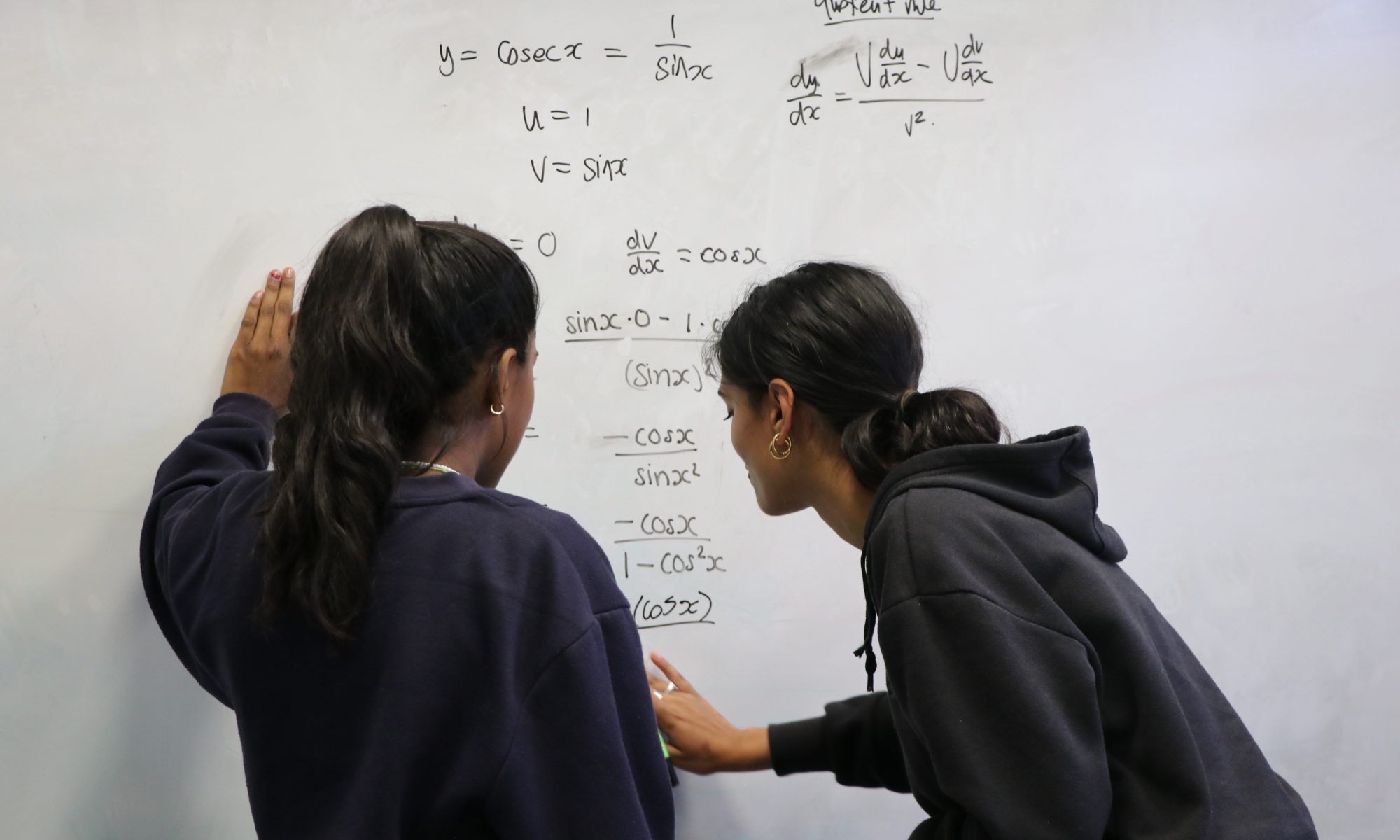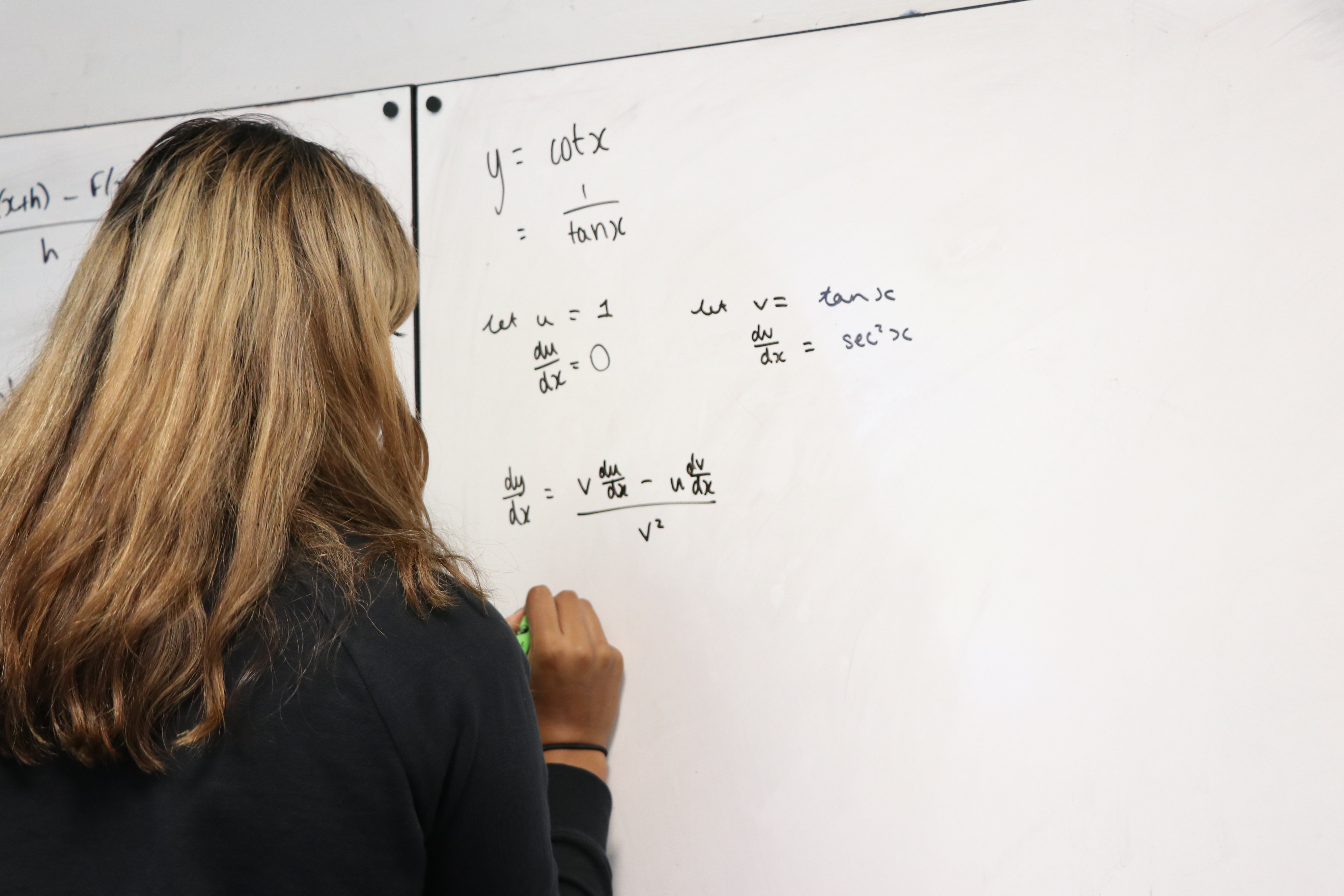Could digital learning be the key to a truly inclusive curriculum?

Mrs Rebecca Brown, GDST Maths Trust Consultant Teacher and Teacher of Maths at WHS, looks at how effective use of digital learning could have the potential to give all students personalised learning experiences.

The use of online video tutorials for learning, especially in Maths, can, if used carefully, provide an individualised learning experience where students study concepts at their own pace, allowing them to review, reflect, pause or accelerate. This in turn enables learners to learn in their own way, giving them more confidence to delve deeper into the subject, embed knowledge and solve problems. Suggestions like this evoke a range of strong emotions and opinions among teachers. Is digital learning the future of education? Or does it mean the de-skilling of teachers and students alike?

How do you learn something new?

If I asked you to learn how to make magic milk, how would you begin? My own first step would be to Google it and watch a top-rated video. Then I would have a go myself. If a student can watch a carefully selected video at their own pace, pause, rewind, replay until they have good understanding of a concept, then surely this is potentially a beneficial personalised learning experience that can be inclusive of the needs of all learners. Moreover, it can help students to overcome anxieties they may face in the classroom.

Video tutorials also give the opportunity for recap, review and consolidation after a lesson or topic has been taught. During the pandemic we saw an increase in online learning and use of video tutorials that supported student and teacher absences and gaps in learning. Now back in the classroom, instead of reverting to what we have always done, what if we considered a different future? How can crisis turn into opportunity, as we use technology in different ways?

Why use digital learning?

Evidence shows that many digital learning resources can be used to develop students’ mathematical capabilities, especially when they are integrated into a rich teaching environment. In a nutshell, the students pre-learn the new content mostly independently, often as homework, and then most of the precious classroom time is spent practicing, asking questions and doing activities with the teacher there to support and guide them.

After watching appropriate, rigorous, considered tutorials, students can engage in richer in-class discussions that help them develop deeper conceptual understanding of Mathematics. This releases lesson time for social interaction, which Vygotsky’s theory of learning as a social process places so much emphasis on.It can also create more time for one-to-one support and direction from teachers. This is a good example of flipped learning, which can be a very powerful pedagogical process.

Fluency gives students the capability to be confident in their calculations and the cognitive capacity to focus on more complex, problem-solving aspects of the curriculum (Foster, 2019).

What could possibly go wrong?

This does all come with an important warning. We need to select the resources that we direct students to use very carefully. I am sure that you know the pitfalls of a YouTube search! This is where selecting and inserting videos into One Note lessons, Google Classroom, Firefly or using resources such as Ed Puzzle can be helpful. Ed Puzzle is an online video editor tool. Your students watch a video, selected by you, at their own pace. You hold every student accountable, observing who is watching and who answers the questions. They are not able to skip ahead or open other tabs. The process is simple – find a video, add questions, and assign it to your class. Watch as they progress, and hold them accountable on their learning journey.

Another drawback is relying solely on digital resources as a method of instruction for students to learn. While flipped learning does give you the opportunity to dive into applying the content rapidly, the teacher must assess learning quickly and be able to rectify misunderstandings. This method also centralises the role of homework. Students need recreation time for holistic development, so it could also become detrimental when only used outside of lessons, as the commitments of learners beyond the classroom could limit the time available, hindering progress. For it to work properly, parents also need to be fully informed and engaged to support this method.

To conclude

We want to empower our learners to become critical thinkers, curious problem solvers and resilient creatives. Perhaps a flipped learning approach, if rigorously thought out and planned, could help address anxieties, give more opportunities to accommodate different learning styles and needs, and give more time for complex, deeper thinking in the classroom. Developed in this way, it could become the future of a truly inclusive education.

You can learn more about Flipped Learning at the GDST EdTech25 event on 25^th May – hosted by Trust Consultant Teachers Fiona Kempton and Rebecca Brown. Sign up here

15th April 20217th June 2022

What is a random number and what is the random number generator?

Sungmin in Year 13 looks at random numbers, explaining what they are and how they are relevant to our lives – from encrypted passwords to how games are programmed.

Random number in real life

As public and private data networks proliferate, it becomes increasingly important to protect the privacy of information. Having a random number is one of the steps which can become a core component of the computer to increase the security of the system platform. Random numbers are important for other things – computer games, for example. Random numbers will ensure there are different consequences after making different decisions during a game. The results will always be different because the given input is different. At an arcade, there are many games that rely on randomness. Falling objects fall in different patterns so that no one can anticipate when to catch the object. Otherwise, some people will be able to calculate how an object will fall and the game will no longer be loved by the people visiting arcades. It is interesting that we get some randomness as such.

The examples such as the falling object and computer games both require random numbers in order to be unique. For those games and many other situations that require randomness, private data must be encrypted. To do so, a true random number plays such a significant role and must be used. On the other hand, when we are programming games, both true random number and pseudo-random numbers can be used. As you might have noticed already, there are two types of random numbers. Random numbers are separated depending on how they are generated. One is the true/real random number and the other is the pseudo-random number.

Definitions of ‘random number’

There are several different ways to define the term, ‘random number’. First of all, it is a number which is generated for, or part of, a set exhibiting statistical randomness. Statistical randomness is a characteristic where a numeric sequence is said to be statistically random when it contains no recognisable patterns or regularities.

Secondly, a random number can be defined as a random sequence that is obtained from a stochastic process. A stochastic or random process can be defined as “a collection of random variables that is indexed by some mathematical set, meaning that each random variable of the stochastic process is uniquely associated with an element in the set.” Moreover, a random number is an algorithmically random sequence in algorithmic information theory. An algorithm is a “process or set of rules to be followed in calculations or other problem-solving operations, especially by a computer”. Also, the sequence which is algorithmically random can be explained as an infinite sequence of binary digits that appears random to any algorithm. The notion can be applied analogously to sequences of any finite alphabet (e.g. decimal digits).

Random sequences are the key object of study in algorithmic information theory. Algorithmic information theory is a merger of information theory and computer science that concerns itself with the relationship between computation and information of computably generated objects, such as strings or any other data structure. Random numbers can also be described as the outputs of the random number generator. In cryptography we define a random number through a slightly different method. We say that the random number is “the art and science of keeping messages secure”.

Different types of random number generators

True random number generator (TRNG)
Hardware true random number generator (HRNG)

Pseudo-random number generator (PRNG)
Linear Congruential Generator
Random number generator in C++

The major difference between pseudo-random number generators (PRNGs) and true random number generators (TRNGs) is easier to understand if you compare and contrast computer-generated random numbers to rolls of a dice. Since the pseudo-random number generator generates random numbers by using mathematical formulae or precalculated lists akin to someone rolling a dice multiple times and writing down all the outcomes, whenever you ask for a random number, you get the next roll of the dice on the list. This means that there are limitless results produced from the list. Effectively, the numbers appear random, but they are in fact predetermined. True random number generators work by “getting a computer to actually roll the dice — or, more commonly, use some other physical phenomenon that is easier to connect to a computer than is a dice”

Comparisons of PRNGs and TRNGs

As you go about your day today, consider how random numbers are being used to support your daily activities – from the passwords we use, the apps we run on our phones, and the devices and programmes we engage with. Maths is all around us.

21st January 20217th June 2022

Why is it socially acceptable to say: “I’m bad at Maths”?

Alys Lloyd, a Maths Teacher at Wimbledon High School, looks at society’s attitude towards Maths, what makes a good mathematician, and how you can compare the retaining of mathematics knowledge to that of languages.

Teachers do have social lives, although to our students this might be a shocking idea. A teacher being spotted outside of school, in the supermarket for example, can send some students into a flat spin. So the idea of a teacher being at a party might be difficult to imagine, but I can assure you, it does happen!

At parties and in social situations with people who don’t know me, I have found that my job can, unfortunately, put a bit of dampener on things. A typical conversation opener is to ask what someone does for a living. The most common response to my saying that I’m a Maths teacher is “oh, wow” then something along the lines of “I was never any good at Maths in school.” Then the person I was talking to politely excuses themselves. I now tend to dodge that kind of question and stick to safer topics.

Why is it socially acceptable to say you are bad at Maths? I doubt that so many people would be so upfront saying that they can’t read… So why does Maths get such bad press?

My Theory

Mathematics is a very black and white subject, with normally only one right answer, although there may be lots of different ways to get there. Many people have been put off Maths because in the past they have got stuck, had a negative experience and not known how to get to the correct solution.

This may have been because the teaching was poor, or the methods they were taught to use didn’t make sense to them, or they didn’t speak up in class so didn’t get help. I believe that by far the most common reason is that they take getting stuck personally. They believe that they didn’t get the right answer because they themselves are bad at Maths. Unfortunately, I don’t think this is something that just happened in the past; it still happens, and I see it happening with the highly achieving girls at WHS. They are not used to getting things wrong, finding something difficult, having to struggle, and they take it personally – they internalise this as a failure: they are bad at Maths.

Which leads us to the question: what makes someone ‘good’ or ‘bad’ at Maths? Who is someone who is ‘good’ at Maths? A Lecturer or Professor of Mathematics? A Maths teacher? Or someone who simply enjoys doing Maths? Is it about who you are comparing yourself to? As a Maths teacher, my level of mathematics is low compared to a Mathematics Professor. Being good at mental arithmetic is not the same as being good at Maths; possibly conversely in fact – professional Mathematicians are notoriously bad at mental arithmetic, as are some Maths teachers!

So, for people who say: “I’m bad at Maths”, they may think that those people who are ‘good’ at Maths never get stuck; never struggle to get to the answer. But I can assure you, that is not the case. I am a Maths teacher and I get stuck on Maths problems. I definitely don’t always immediately know how to get to the answer.

I believe the difference in how you feel about Maths is about what you do when you get stuck, because we ALL get stuck. Being stuck isn’t bad – it’s part of the process. It is a way of forming new connections in the brain; it’s a part of learning.

When I get stuck on a problem I don’t take it personally; I don’t take it as a reflection of my mathematical ability; I think of it as a challenge, a conundrum to be figured out, a puzzle to be solved. If I can’t find a solution quickly, I stop and try to think about it differently. Could it be thought about in another way? Can I visualise it by drawing a sketch or diagram? Is there an alternative approach or method I haven’t tried? Have I used all the information I have available? These are very important problem-solving skills and have lots of relevance to everyday life.

Use it or lose it

Mathematics in many ways can be considered its own language. When learning languages, you start with basics: hello, please, thank you, and a few important sentences (dos cervezas, por favor); and build up to be able to communicate fluidly. If you have ever tried to learn a language seriously, you will know that it is not a smooth process. You go through phases of thinking you’re doing great, then you feel like you plateau – you realise that there is a whole verb tense you had no idea existed, that you now need to learn.

Maths is similar. You need to know the basics: numbers, patterns, arithmetic, and a few important ideas like algebra; and you build up to some quite complicated Maths like calculus, proof, complex numbers. With Maths numbers and algebra are the words, and rules like BIDMAS are the grammar. They are a means to the same end as languages – to communicate effectively.

One aspect of learning a language (or learning a musical instrument) is that if you don’t practise it regularly, you start to lose the gains you had made; it becomes more difficult, and eventually you forget. I firmly believe – that like a language – if you don’t use Maths, if you don’t practise it regularly, you start to lose it.

For me, this explains why parents can struggle to remember how to do school-level Maths with their children, even if they found it easy when they were young – they haven’t practised it in years. It can seem like an alien language – it’s hard to pick something up again when you have had such a long gap.

Yet even if you, yourself, haven’t used Maths in years, you are constantly using things that have been programmed by someone using Mathematics. Maths underpins everything ‘modern’ around us: the computer at which I am typing this article, the smartphone in your pocket; it keeps planes in the air and stops them crashing into each other; it’s in our buildings, in our clothes; Maths is fundamental to our modern style of living.

We want to encourage our children to feel it is socially unacceptable to be bad at Maths. We want them to be the ones solving the problems of the future, and part of this will certainly require mathematics.

So, what’s the take-home message? I’d like to think it’s this: in Maths, as in life, we all get stuck, but the people who succeed are the ones who don’t give up. And if you are lucky enough to meet a Maths teacher at a party, please be nice!

Above: Photo by Kaboompics .com from Pexels

6th February 20207th June 2022

The proof behind one of the most famous theorems in mathematics

Vishaali, Year 10, looks behind the proof of one of the most famous mathematical theorems – that of Pythagoras’ theorem.

What is the difference between a theorem and a theory?

A theorem is a mathematical statement that has been proven on the basis of previously established statements. For example, Pythagoras’ theorem uses previously established statements such as all the sides of a square are equal, or that all angles in a square are 90°. The proof of a theorem is often interpreted as justification of the statement that the theorem makes.

On the other hand, a theory is more of an abstract, generalised way of thinking and is not based on absolute facts. Examples of theories include the theory of relativity, theory of evolution and the quantum theory. Take the theory of evolution; this is about the process by which organisms change over time as a result of heritable behavioural or physical traits. This is based on undeniable true facts, but more from experience and from an abstract way of thinking.

It is also important not to confuse mathematical theorems with scientific laws as they are scientific statements based on repeated experiments or observations.

The proof behind Pythagoras’ theorem

You have probably all heard of Pythagoras’ theorem, one of the simplest theorems there is in mathematics, that is relatively easy to remember. Given that it’s so easy to remember and to learn, wouldn’t it be an added bonus to know exactly how this theorem came to be?

The theorem, a²+b²=c², relates the sides of any right-angled triangle enabling you to find the lengths of any side, given you have the lengths of the other two.

This whole theorem is based on a triangle like this:

These four right-angled triangles are exactly the same just rotated slightly differently to create this shape:

Two shapes have been made by putting these triangles in this order. A big square on the outside, and another slightly smaller square in the middle. As all these triangles are the exact same you can label them A, B and C.

You can tell from the labels the triangles have been given, that the bigger square would have the sides (a+b), and the smaller triangle in the middle will have sides of c. Therefore we know the area of the smaller square is c² :

Using the exact same four triangles, we can rotate and translate them to create a slightly different shape:

Now two more squares have been added to this shape. We can call them a² and b².

Thinking back to the shape we made before, we can also see that the length of this shape is also (a+b). As we know we used the same four right-angled triangles for the shape before and now, we can infer that the two squares a² and b² are exactly the same as the square from the first shape, c². Hence we get Pythagoras’ theorem, a²+b²=c²:

References:

https://www.livescience.com/474-controversy-evolution-works.html
https://www.askdifference.com/theorem-vs-theory/