Posted on

What is a random number and what is the random number generator?

Dice

Sungmin in Year 13 looks at random numbers, explaining what they are and how they are relevant to our lives – from encrypted passwords to how games are programmed.

Random number in real life

As public and private data networks proliferate, it becomes increasingly important to protect the privacy of information. Having a random number is one of the steps which can become a core component of the computer to increase the security of the system platform. Random numbers are important for other things – computer games, for example. Random numbers will ensure there are different consequences after making different decisions during a game. The results will always be different because the given input is different. At an arcade, there are many games that rely on randomness. Falling objects fall in different patterns so that no one can anticipate when to catch the object. Otherwise, some people will be able to calculate how an object will fall and the game will no longer be loved by the people visiting arcades. It is interesting that we get some randomness as such.

The examples such as the falling object and computer games both require random numbers in order to be unique. For those games and many other situations that require randomness, private data must be encrypted. To do so, a true random number plays such a significant role and must be used. On the other hand, when we are programming games, both true random number and pseudo-random numbers can be used. As you might have noticed already, there are two types of random numbers. Random numbers are separated depending on how they are generated. One is the true/real random number and the other is the pseudo-random number.

Definitions of ‘random number’

There are several different ways to define the term, ‘random number’. First of all, it is a number which is generated for, or part of, a set exhibiting statistical randomness. Statistical randomness is a characteristic where a numeric sequence is said to be statistically random when it contains no recognisable patterns or regularities.

Secondly, a random number can be defined as a random sequence that is obtained from a stochastic process. A stochastic or random process can be defined as “a collection of random variables that is indexed by some mathematical set, meaning that each random variable of the stochastic process is uniquely associated with an element in the set.”  Moreover, a random number is an algorithmically random sequence in algorithmic information theory. An algorithm is a “process or set of rules to be followed in calculations or other problem-solving operations, especially by a computer”. Also, the sequence which is algorithmically random can be explained as an infinite sequence of binary digits that appears random to any algorithm. The notion can be applied analogously to sequences of any finite alphabet (e.g. decimal digits).

Random sequences are the key object of study in algorithmic information theory. Algorithmic information theory is a merger of information theory and computer science that concerns itself with the relationship between computation and information of computably generated objects, such as strings or any other data structure. Random numbers can also be described as the outputs of the random number generator. In cryptography we define a random number through a slightly different method. We say that the random number is “the art and science of keeping messages secure”.

Different types of random number generators

1:

  • True random number generator (TRNG)
  • Hardware true random number generator (HRNG)

2:

  • Pseudo-random number generator (PRNG)
  • Linear Congruential Generator
  • Random number generator in C++

The major difference between pseudo-random number generators (PRNGs) and true random number generators (TRNGs) is easier to understand if you compare and contrast computer-generated random numbers to rolls of a dice. Since the pseudo-random number generator generates random numbers by using mathematical formulae or precalculated lists akin to someone rolling a dice multiple times and writing down all the outcomes, whenever you ask for a random number, you get the next roll of the dice on the list. This means that there are limitless results produced from the list. Effectively, the numbers appear random, but they are in fact predetermined. True random number generators work by “getting a computer to actually roll the dice — or, more commonly, use some other physical phenomenon that is easier to connect to a computer than is a dice”

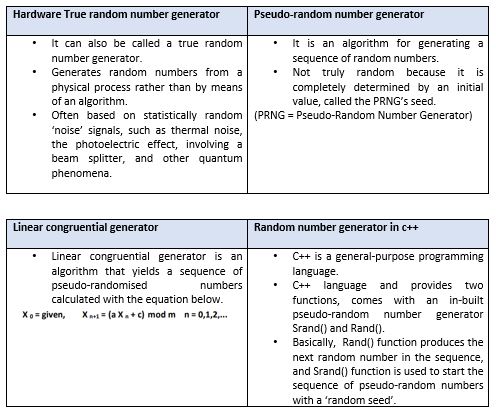
Comparisons of PRNGs and TRNGs

As you go about your day today, consider how random numbers are being used to support your daily activities – from the passwords we use, the apps we run on our phones, and the devices and programmes we engage with. Maths is all around us.

Posted on

To infinity and beyond! Understanding more about the concept of infinity

Elena, Year 13, explores the concept of infinity, challenging our understanding.

Most people nowadays are comfortable with the idea that numbers can go on forever. Theoretically, you could keep counting on and on.

If I asked: Which is bigger? The set of all counting numbers, or the set of all even numbers?

Above: Infinity symbol (Wikipedia)

The natural inclination would be to say that the set of all numbers is larger than the set of even numbers. However, these two sets of infinities are actually equal.

Hilbert’s Hotel Paradox

In the 1920s, the German mathematician David Hilbert devised a famous thought experiment to show us just how hard it is to wrap our minds around the concept of infinity.

Imagine a grand hotel with an infinite number of rooms and an infinite number of guests in those rooms.

To challenge the common idea about infinity, he asked what would happen if a new guest came along and asked to stay in a room. At first, it seems impossible, as there is already an infinite number of guests.

However, the trick is to ask each guest to move along one room:

The guest in room 1 moves to room 2, the one in room 2 moves to room 3 and so on. Since there is an infinite number of rooms, there will still be room for all the previous guests.

So the new guest would have a space in room number 1. This shows that infinity+1 is still equal to infinity.

This solution is only possible because the infinite hotel only deals with the lowest levels of infinity, mainly the countable infinity of the natural numbers.

Cardinality

If we were dealing with higher orders of infinity, such as the real numbers, these strategies would not be possible as there is no way of systematically including every number.

The infinite hotel on the real number line would have an infinite number of rooms in the basement (negative numbers), fractional rooms, square root rooms and other irrational number rooms.

Even though this example shows how adding infinities equals another infinity, some infinities are known to be bigger than others.

This concept was first introduced in 1891 by a German mathematician called Georg Cantor, who tackled the idea of the existence of transfinite numbers and their cardinality.

Transfinite numbers are numbers which are used to describe the size of an infinite set of numbers, while cardinality is the size of a set.

Having the same cardinality means that there is a one-to-one correspondence between sets of numbers – this is called a bijection. This means that each number from one set can be matched up with a number in another set.

Conclusion

In summary, when adding infinities together, you get another infinity. However, this new infinity will have the same cardinality as the previous one. This is because it will be possible to make a bijection with the original infinities.

On the other hand, there are infinities which are so large, that their cardinality (known as 𝖈) is still considered to be a hypothesis, and anything between the smallest cardinality and the largest one is still a mystery to be proved.

This shows how hard it is for our finite minds to imagine a concept as large as infinity.

Bibliography

Alfeld, Peter. (1996). Why are there infinitely many prime numbers?. Available: https://www.math.utah.edu/~pa/math/q2.html .

Crowston, Robert. (2011). Hilbert’s Hotel. Available: https://nrich.maths.org/5788 .

Jaksich, John. (2013). Infinity is Weird. Available: https://skullsinthestars.com/2013/11/14/infinity-is-weird-how-big-is-infinity/ .

Marianne. (2013). Maths in a Minute: Countable Infinities. Available: https://plus.maths.org/content/maths-minute-countable-infinities .

Mcgregor, Peter. (2008). A glimpse of Cantor’s Paradise. Available: https://plus.maths.org/content/glimpse-cantors-paradise .

Posted on

Can the Harkness approach to delivering Maths lead to a deeper understanding?

Mrs Clare Duncan, Director of Studies at WHS @MATHS_WHS, describes the Harkness approach she observed at Wellington College and the impact that this collaborative approach has in the understanding of A Level Maths.

Named after its founder, Edward Harkness, Harkness it is a pedagogical approach that promotes collaborative thinking. Edward Harkness’ view was that learning should not be a solitary activity instead it would benefit from groups of minds joining forces to take on a challenging question or issue. What Harkness wanted was a method of schooling that would train young people not only to confer with one another to solve problems but that would give them the necessary skills for effective discussion. Harkness teaching is a philosophy that began at Philips Exeter Academy in New Hampshire in the 1930s.

Edward Harkness stated:

“What I have in mind is [a classroom] where [students] could sit around a table with a teacher who would talk with them and instruct them by a sort of tutorial or conference method, where [each student] would feel encouraged to speak up. This would be a real revolution in methods.”

This was very much what the classroom looked like when I was lucky enough to observe Maths teaching at Wellington College last term. Their newly refurbished Maths rooms had floor to ceiling whiteboards on all the walls. On entering the classroom, the students were already writing their solutions to problems that were set at preparatory work for the lesson. Whether the solution was correct or not was irrelevant, it was a focal point which allowed students to engage in discussion and offer their own views, problems and suggestions. The discussion was student led with the teacher only interjecting to reinforce a significant Maths principle or concept.  The key learning point is giving the students their own time before the lesson to get to grips with something before listening to the views of others.

The Maths teachers at Wellington College have developed their own sets of worksheets which the students complete prior to the lesson. Unlike conventional schemes of work, the worksheets follow an ‘interleaving’ approach whereby multiple topics are studied at once. Time is set aside at the start of the lesson for students to put their solutions on whiteboards, they then walk around the room comparing their solutions to those of others. Discussion follows in which students would discuss how they got to their answers and why they selected the approach they are trying to use. In convincing others that their method was correct, there was a need for them to justify mathematical concepts in a clear and articulate manner. The students sit at tables in an oval formation, they can see one another and no-one is left out of the discussion. The teacher would develop the idea further by asking questions such as ‘why did this work?’ or ‘where else could this come up?’.

The aim of Harkness teaching is to cultivate independence and allows student individual time to consume a new idea before being expected to understand it in a high-pressured classroom environment. This approach can help students of all abilities. Students who find topics hard have more time than they would have in class to think about and engage with new material and students who can move on and progress are allowed to do so too. In class, the teacher can direct questioning in such a way that all students feel valued and all are progressing towards the end objectives.  It involves interaction throughout the whole class instead of the teacher simply delivering a lecture with students listening. It was clear that the quality of the teachers questioning and ability to lead the discussion was key to the success of the lesson.

Figure 1: WHS pupils in a Maths lesson solving problems using the Harkness approach

This was certainly confirmed by my observations. The level of Maths discussed was impressive, students could not only articulate why a concept worked but suggested how it could be developed further. I was also struck by how students were openly discussing where they went wrong and what they couldn’t understand; a clear case of learning from your mistakes. Whenever possible the teaching was student led. Even when teachers were writing up the ‘exemplar’ solutions, one teacher was saying ‘Talk me through what you want me to do next’. Technology was used to support the learning with it all captured on OneNote for students to refer to later. In one lesson, a student was selected as a scribe for notes. He typed them up directly to OneNote; a great way of the majority focusing on learning yet still having notes as an aide memoir.

Although new to me, at Wimbledon we have been teaching using the Harkness approach to the Sixth Form Further Maths students for the past couple of years. Having used this approach since September it has been a delight to see how much the Year 12 Further Maths pupils have progressed. Being able to their articulate mathematical thinking in a clear and concise way is an invaluable skill and, although hesitant at first, is now demonstrated ably by all the students. The questions posed and the discussions that ensue take the students beyond the confinements of the specifications.

–

References
https://learning.wellingtoncollege.org.uk/harkness-teaching-and-uk-education/